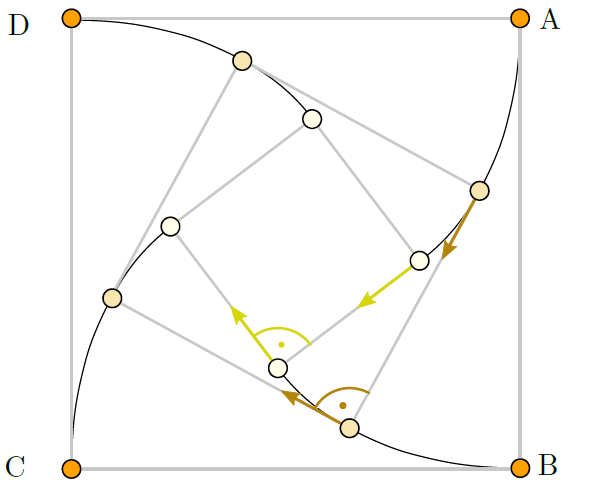
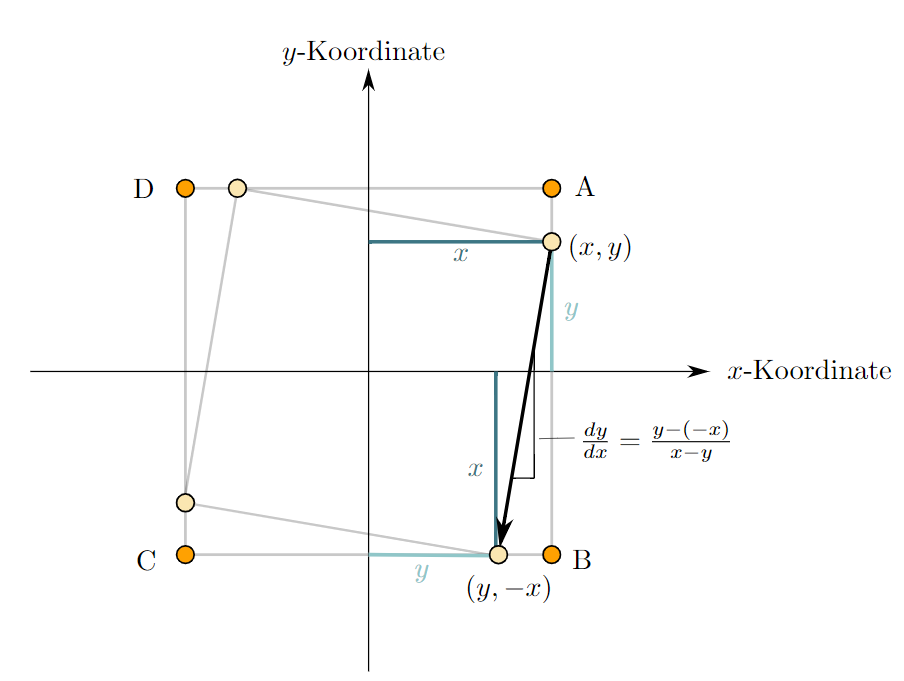
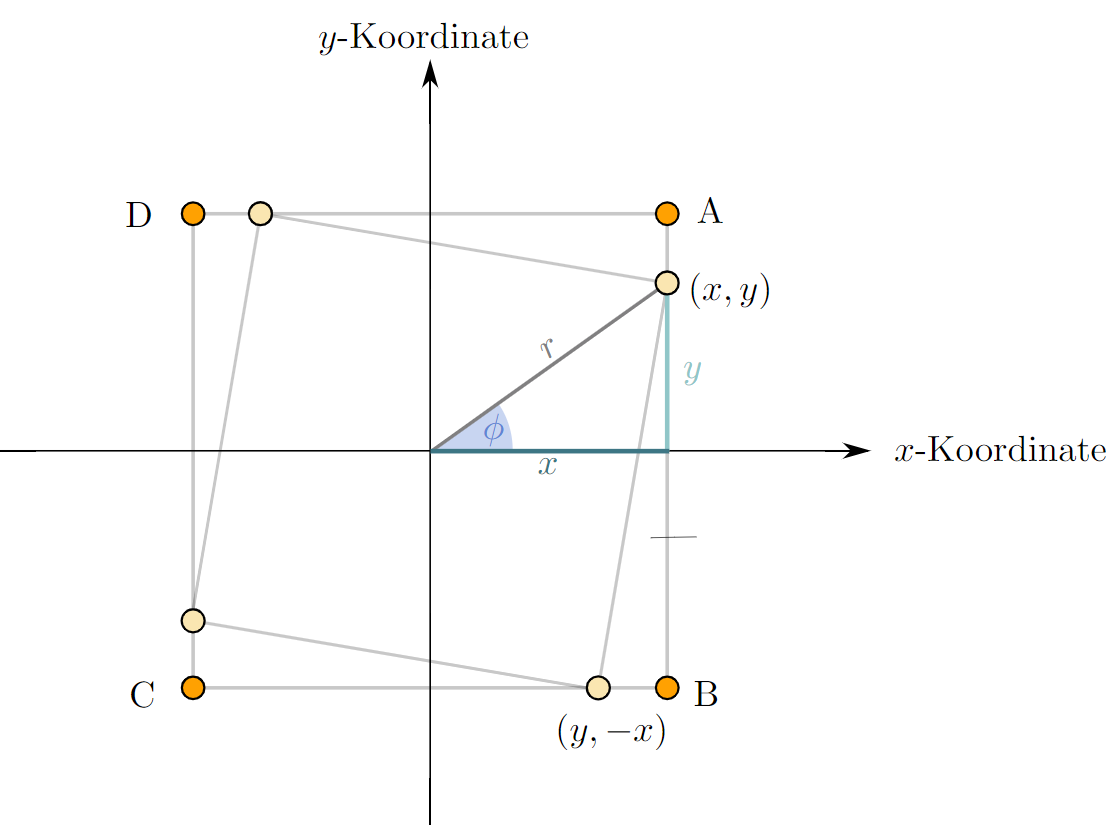
Zu jedem Zeitpunkt der Verfolgung sitzen die 4 Käfer auf den Ecken eines Quadrats, welches sich immer kleiner werdend um den Ursprung dreht. Die Bewegungsrichtung eines verfolgenden Käfers steht daher stets senkrecht auf der Bewegungsrichtung des verfolgten Käfers. Während der Bewegungsvektor von Käfer A stets auf Käfer B zeigt, sich Käfer A also zu jedem Zeitpunkt auf Käfer B zubewegt, ist die Bewegungsrichtung von Käfer B stets senkrecht dazu. Folglich gibt es keinen Anteil der Bewegung von Käfer B, der Käfer B näher oder weiter weg von Käfer A bringt. Ausschließlich Käfer A bewegt sich auf Käfer B zu. Das heißt, der Weg, den Käfer A zurücklegen muss, um Käfer B zu erreichen, ist genauso lang, wenn beide sich bewegen, wie wenn Käfer B an seiner Ecke stehen bleibt. Der Weg beträgt also die Seitenlänge des Quadrats der Startformation.

Eine Differentialgleichung (DGL) ist eine Gleichung für eine gesuchte Funktion, in der auch Ableitungen der gesuchten Funktion vorkommen.

Um die Differentialgleichung für den Weg unserer Käfer zu finden, müssen wir mathematisch modellieren. Das geht so: Die Abbildung zeigt in Orange die Startformation der Käfer und in Hellorange die Formation der Käfer nach einem (großen) Schritt. Mit $(x,y)$ beschreiben wir die Position von Käfer A. Aus der Symmetrie folgt für die Position des Käfers B zu $(y,-x)$, wobei $y$ und $x$ die Koordinaten von Käfer A sind.

Käfer A verfolgt Käfer B, d.h. der Richtungsvektor von Käfer A zeigt immer zu Käfer B. Hier gekennzeichnet als der schwarze Pfeil. Die Steigung des Richtungsvektors, welche gleichzeitig die Tangente an die Kurve von Käfer A ist, ergibt sich zu

\[ \begin{align} \frac{dy}{dx}%=\frac{y-(-x)}{x-y}= =\frac{x+y}{x-y} . \end{align} \]

Damit wir die DGL lösen können, müssen wir clever substituieren. Die Idee ist $y=w(x)\cdot x$ zu verwenden. Die linke Seite der Gleichung wird zu

\[ \begin{align*} \frac{dy}{dx}=\frac{d(w\cdot x)}{dx}=\frac{dw}{dx}x+w\frac{dx}{dx}=\frac{dw}{dx}x+w. \end{align*} \]

Die rechte Seite der Gleichung wird zu

\[ \begin{align*} \frac{x+y}{x-y}=\frac{x+w\cdot x}{x-w\cdot x}= \frac{1+w}{1-w}. \end{align*} \]

Damit lautet unsere neue DGL mit der Variablen $w(x)$

\[ \begin{align} \frac{dw}{dx}x+w=\frac{1+w}{1-w}. \end{align} \]

Die neue DGL lässt sich nun mit dem Schema „Trennung der Variablen“ lösen. Hierzu bringen wir alle Terme die abhängig von $x$ sind auf die eine und alle die abhängig von $w$ sind auf die andere Seite. Wir erhalten formal

\[ \frac{1-w}{1+w^2} \,dw = \frac{1}{x} \,dx \] und lösen durch Integrieren \[ \begin{align*} \int \frac{1-w}{1+w^2} \,dw = \int \frac{1}{x} \,dx. \end{align*} \]

Mit den jeweiligen Stammfunktionen erhalten wir

\[ \begin{align*} \arctan(w)-\frac{1}{2}\ln(1+w^2)=\ln(x)+c, \end{align*} \]

mit $c$ als Integrationskonstante. Rücksubstituieren mit $w=\frac{y}{x}$ und Umstellen, ergibt

\[ \begin{align} \arctan(\frac{y}{x})=\frac{1}{2}\ln(1+\frac{y^2}{x^2})+\ln(x)+c. \end{align} \]

Wir können die Integrationskonstante $c$ aus der Startformation berechnen. In unserem Beispiel: Käfer A startet an der Position $(x,y)=(0.5 ,0.5)$. Nach Einsetzen erhalten wir

\[ \begin{align*} \arctan(1)=\frac{1}{2}\ln(1+1)+\ln(0.5)+c\\ c= \arctan(1)-\ln(\sqrt{0.5})= \frac{\pi}{4}-\ln(\sqrt{0.5}). \end{align*} \]

Setzen wir nun die Integrationskonstante $c$ in die Stammfunktion ein, erhalten wir, dass Käfer A auf folgender Kurve krabbelt

\[ \begin{align} \arctan(\frac{y}{x})=\ln(\sqrt{x^2+y^2})+\frac{\pi}{4}-\ln(\sqrt{0.5}). \end{align} \]

Mit $r$ beschreiben wir den Abstand des Käfers vom Ursprung, mit $\phi \in (-\infty,\frac{\pi}{4}]$ den Winkel zwischen Käfer A und der $x$-Achse. Mit jeder Umdrundung des Käfers um den Ursprung wird $\phi$ um $2\pi$ kleiner, denn der Käfer läuft mit dem Uhrzeigersinn.

Der Abstand $r$ zum Ursprung entspricht dem Betrag des Vektors $(x,y)$. Es gilt daher: $r^2=x^2+y^2$. Wie aus der Abbildung zu erkennen, gilt: $\arctan(\frac{y}{x})=\phi$. Eingesetzt erhalten wir:

\[ \begin{align*} \phi = \ln(r)+\frac{\pi}{4}-\ln(\sqrt{0.5}). \end{align*} \]

Nach $r$ umgestellt folgt

\[ \begin{align*} r= \sqrt{0.5} \cdot e^{\phi-\frac{\pi}{4}}. \end{align*} \]

Wir haben es mit einer sogenannten logarithmischen Spirale zu tun.

Die vier Käfer sind auf verschiedenen logarithmischen Spiralen unterwegs, die sich nicht überschneiden und sich unendlich oft um den Ursprung winden. Sie nähern sich dabei immer weiter dem Ursprung an und erreichen diesen für $\phi \rightarrow -\infty$. Rechnerisch erhalten wir: \[ \lim_{\phi \rightarrow -\infty} r(\phi)= \lim_{\phi \rightarrow -\infty} \sqrt{0.5} \cdot e^{\phi-\frac{\pi}{4}} = 0.\] Das heißt, im Grenzwert geht der Radius gegen 0.

Der Weg den jeder Käfer dabei zurücklegt, ist endlich (Eigenschaft 4 der logarithmischen Spirale). Die Länge des Weges ergibt sich aus der Bogenlänge der Spirale oder anhand der Überlegung aus dem Abschnitt Problemstellung.