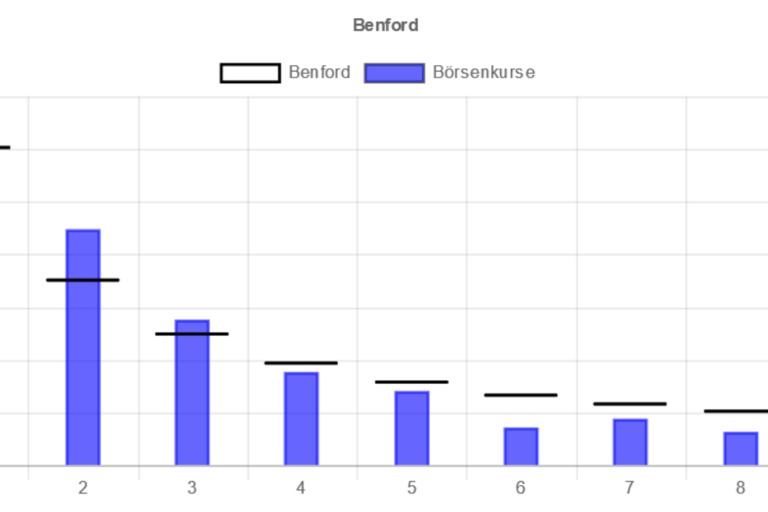
Digitale Exponate zum Ausprobieren
Unsere Studierenden der Fakultät für Informatik und Mathematik haben verschiedene Themen aus der Mathematik und der Informatik zum Ausprobieren aufbereitet. Wir wollen euch Spannendes und Kniffliges aus unseren Fachgebieten zeigen.
Zu den folgenden Kategorien kannst du interessante Themen aus der Mathematik und der Informatik interaktiv erforschen:
Interaktive Applets
Vorstellung von Hands-On Exponaten
Digitale Poster
Entdecke Poster zu interessanten Themen aus der Mathematik und der Informatik:
Wie funktioniert der QR-Code?
Überall begegnen uns diese seltsamen Muster aus lauter schwarzen und weißen Quadraten, die scheinbar wahllos hingewürfelt wurden. Was steckt dahinter?
Dieser Frage hat sich Stefan Becher angenommen. Zum Poster.
Betreuung: Prof. Dr. Brigitte Forster-Heinlein
Wie funktioniert der QR-Code?
Mechanisch Integrieren? Gibt es wirklich Geräte, mit welchen man die Größe beliebiger ebener Flächenformen bestimmen kann?
Ja, das gibt es. Antonia Knötig hat die Antwort.
Betreuung: Prof. Dr. Brigitte Forster-Heinlein
Mechanisch Integrieren
Wie bohrt man eckige Löcher? Wie gestaltet man ein Objekt, das überall gleich dick sein soll, mit möglichst wenig Material?
Monique Schunder hat den Schlüssel zu diesen Fragen - die Gleichdicke - vorgestellt und erklärt, wie die britischen 20- und 50-Pence Münzen zu ihrer besonderen Form gekommen sind.
Betreuung: Prof. Dr. Brigitte Forster-Heinlein
Gleichdicke – Kurven und Körper konstanter Breite
Unterlagen zum Download
von Lisa Gaspar
Betreuung: Lena Bachl und Prof. Dr. B. Forster
Die Spieltheorie als Teilgebiet der Mathematik ist eine Theorie sozialer Interaktion. Im Mittelpunkt dieser Wissenschaft stehen Kontexte, in denen das Ergebnis einer Entscheidung in Abhängigkeit vom eigenen, aber auch vom Verhalten der anderen Spieler definiert wird. In erster Linie beschäftigt sich die Spieltheorie damit, für ein gegebenes Spiel eine Lösung zu ermitteln.
Ein populäres Beispiel ist das Spiel Schere, Stein, Papier. Dieses wird von 2 Spielern durchgeführt, welche sich unabhängig voneinander für eine Strategie entscheiden. Beide Spieler können jeweils entweder Schere, Stein oder Papier wählen. Folgende Regeln gelten: Schere schneidet Papier, Papier bedeckt Stein, Stein schleift Schere.
Wählt also beispielsweise Spieler 1 die Strategie Schere und Spieler 2 Papier, so gewinnt Spieler 1 während Spieler 2 verliert. Ausgehend von der Annahme, dass bei Verlust 1 Euro an den Gegenspieler abzugeben sind und bei
Gleichstand nichts passiert, erhalten wir die unten stehende Auszahlungsmatrix für Spieler 1 (analog für Spieler 2).
Unterrichtsmaterialien:
- Interaktives Spiel zum Gefangenendilemma
- Kurzer Theorieteil zum Nash-Gleichgewicht
- Anwendungsbeispiel 1 und Anwendungsbeispiel 2 für das Nash-Gleichgewicht, mit denen sich die Schülerinnen und Schüler eigenständig beschäftigen können.
Die Unterrichtsmaterialien sind geeignet für Schülerinnen und Schüler der Unter- und Mittelstufe in allen weiterführenden Schulen. Ihr Einsatz ist vor allem für Themenstunden, Vertretungsstunden, oder die letzten Stunden vor den Ferien geeignet. Da die Thematik der Spieltheorie in deutschen Lehrplänen nicht vorzufinden ist, sind die Materialien so gestaltet, dass kein Vorwissen notwendig ist. Dadurch können die Unterrichtsstunden sowohl in der fünften, aber auch beispielsweise in der zehnten Jahrgangsstufe gehalten werden.
Das Nash-Gleichgewicht in der Spieltheorie
von Jacqueline Griebl
Betreuung: Lena Bachl und Prof. Dr. B. Forster
Die Lagrange-Methode ist neben der in der Schule behandelten Variablensubstitution ein Lösungsverfahren für Extremwertaufgaben.
Nach didaktischer Reduktion und einer vorherigen Behandlung des partiellen Ableitens könnte die Lagrange-Methode auch bei Anwendungen der Differentialrechnung in der gymnasialen Oberstufe sowie an Fach- und Berufsoberschulen zum Einsatz kommen.
Die im Rahmen des Seminars entwickelten Unterlagen enthalten Erklärungen und Aufgaben zum partiellen Ableiten sowie zur Lagrange-Methode. Sie können als pdf oder docx Datei heruntergeladen werden:
Diese Seite teilen
